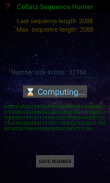


Collatz Sequence Hunter (3n+1)

Deskripsi Collatz Sequence Hunter (3n+1)
If n is even, then divide it by 2 to obtain n/2. If n is odd, then multiply it by 3 and add 1 to obtain 3n+1.
Collatz conjecture states that if you start with any positive integer n and repeat this process indefinitely, then eventually this Collatz sequence will reach 1.
However, it is not known whether Collatz conjecture is true and hence it is an open problem. As of 2017, the conjecture has been checked by a computer for the values of up to 87 * 2^60. Therefore, an experimental evidence suggests that it should be true. However, sometimes one can find only very large example to some mathematical problems. For example, Pólya conjecture has a counterexample of around 1.845 × 10^361. Other examples include Mertens conjecture and Skewes's number.
Collatz Sequence Hunter app will generate a random starting number up to 8192 bits long, equivalently up to 2^8192 or approximately up to 10^2466. Subsequently, the Collatz sequence is computed until 1 is reached. For the largest numbers allowed, this usually takes a few minutes at most. The sequence length from the start until 1 is reached is recorded. The last and maximum sequence lengths are displayed.
But what if the Collatz sequence for your generated number never reaches 1? Then you are very lucky, go and celebrate: you found a contradiction to Collatz conjecture!!!
But hey, what about your phone, will it go on to compute forever? What about your lucky number, can you recover it? When Collatz Sequence Hunter app crosses a certain magical number of steps in computation, then it will stop and save the number automatically. So do not stop the phone or turn off the app, just be patient!
Who knows? Maybe the next breakthrough in mathematics will be made by a toddler!